
Не знаю кому как, но мне очень нравятся работы Эшера. Строгость и математичность картин задевает какую-то струну в душе. Очень хочется попробовать сделать что-то такое-же, но сказывается обделенность художественным талантом. Тем не менее, поиски привели к весьма простой технике, позволяющей любому желающему создавать взаимосвязанные геометрические изображения
Повторяющиеся элементы, такие как ящерицы, могут стать основой многих изделий. Например, можно их использовать в мозаике, декоративных и сувенирных элементах, тротуарной плитке и т.п. Это на первый взгляд, кажется, что нарисовать подобное их под силу только гениальному художнику, либо мощному компьютеру. На самом деле все наоборот. Любой человек, сносно владеющий работой в векторных редакторах, или хотя бы карандашом и циркулем, способен самостоятельно создать элементы, соединяющиеся друг с другом по сложной кривой.
Основу всех геометрических фигур, с взаимосопрягаемыми сторонами составляют три базовых примитива – равносторонний треугольник, квадрат и правильный шестиугольник. Только эти элементы могут плотно располагаться на плоскости, т.е. без свободного пространства между отдельными фигурами. Для построения изображений, которые можно сопрягать между собой, можно использовать любой из примитивов. Ниже будет показан пример с использованием шестиугольника. Именно он лег в основу знаменитых Ящериц.
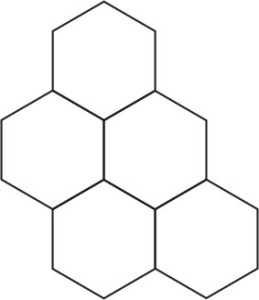
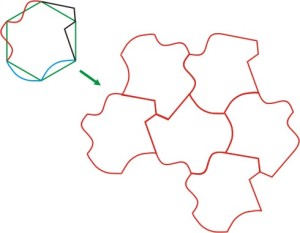
Принцип построения сопрягаемых элементов относительно прост. Выпуклость должна соответствовать вогнутости и наоборот. Эшер для такого построения использовал принцип поворота. Для этого, на одной из сторон шестиугольника рисуется необходимая кривая. Начало и конец кривой должны лежать в вершинах фигуры. Затем, полученная кривая простым поворотом переносится на соседнюю сторону. Центр вращения должен лежать в вершине шестиугольника. Подобным действие получается две одинаковых кривых, которые затем станут контуром фигуры. Для оставшихся четырех сторон выполняется аналогичное действие. Далее основа фигуры (шестиугольник) удаляется. Результатом становится контур, поворачивая и располагая который, можно создать плотный геометрический рисунок. Подобным же образом получается строить сопрягаемые контуры с использованием основы в виде квадрата. Треугольник потребует несколько иного подхода.
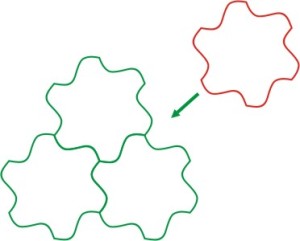
Если использовать только одну кривую, последовательно перенося ее на все грани, результат будет выглядеть как псевдо-правильный многоугольник. Построение более сложных изображений потребует некоторого художественного видения и экспериментов. Тем не менее, используя описанный принцип можно получить огромное количество разнообразных фигур, которые сопрягаясь друг с другом, дадут удивительное изображение, состоящее из одинаковых элементов.
В завершении маленькое замечание. Для построения сложных фигур лучше всего использовать не векторный редактор, а программы машиностроительного черчения. Они имеют гораздо более удобные инструменты для проведения подобных работ и более точно сохраняют геометрию кривых.


 23 января, 2013
23 января, 2013 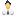 CNC
CNC 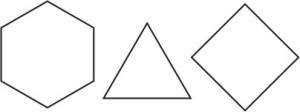
 Posted in
Posted in  Tags:
Tags: